В данном курсе будет описан алгоритм обратного распространения ошибок на примере двух небольших нейронных сетей, реализованных на Python.
Каждная нейронная сеть, тренируемая через обратное распространение (backpropagation), пытается использовать входные данные для предсказания выходных.
Обратное распространение, в самом простом случае, рассчитывает статистическое соответствие между входными и выходными данными для создания модели.
Нейросеть в два слоя
import numpy as np
# sigmoid function
def nonlin(x,deriv=False):
if(deriv==True):
return x*(1-x)
return 1/(1+np.exp(-x))
# input dataset
X = np.array([ [0,0,1],
[0,1,1],
[1,0,1],
[1,1,1] ])
# output dataset
y = np.array([[0,0,1,1]]).T
# seed random numbers to make calculation
# deterministic (just a good practice)
np.random.seed(1)
# initialize weights randomly with mean 0
syn0 = 2*np.random.random((3,1)) – 1
for iter in range(10000):
# forward propagation
l0 = X
l1 = nonlin(np.dot(l0,syn0))
# how much did we miss?
l1_error = y – l1
# multiply how much we missed by the
# slope of the sigmoid at the values in l1
l1_delta = l1_error * nonlin(l1,True)
# update weights
syn0 += np.dot(l0.T,l1_delta)
print(“Output After Training:”)
print(l1)
Output After Training:
[[ 0.00966449]
[ 0.00786506]
[ 0.99358898]
[ 0.99211957]]
Переменные и их описания.
X — матрица входного набора данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети или скрытый слой
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
“*” — поэлементное умножение – два вектора одного размера умножают соответствующие значения, и на выходе получается вектор такого же размера
“-” – поэлементное вычитание векторов
x.dot(y) – если x и y – это вектора, то на выходе получится скалярное произведение. Если это матрицы, то получится перемножение матриц. Если матрица только одна из них – это перемножение вектора и матрицы.
Разбор кода построчно
import numpy as np
Данной строчкой импортируется numpy, библиотека линейной алгебры.
def nonlin(x,deriv=False)
Данная функция создаёт «сигмоиду». Она ставит в соответствие любое число значению от 0 до 1 и преобразовывает числа в вероятности, а также имеет несколько других полезных для тренировки нейросетей свойств.

Эта функция также умеет выдавать производную сигмоиды (deriv=True). Это одно из её полезных свойств. Если выход функции – это переменная out, тогда производная будет out * (1-out).
X = np.array([ [0,0,1],
[0,1,1],
[1,0,1],
[1,1,1] ])
Инициализация массива входных данных в виде numpy-матрицы. Каждая строка – тренировочный пример. Столбцы – это входные узлы. В данном случае получается 3 входных узла в сети и 4 тренировочных примера.
y = np.array([[0,0,1,1]]).T
Инициализирует выходные данные. “.T” – функция транспонирования. После транспонирования у матрицы y есть 4 строки с одним столбцом. Как и в случае входных данных, каждая строка – это тренировочный пример, и каждый столбец (в данном случае один) – выходной узел. У сети получается 3 входа и 1 выход.
np.random.seed(1)
Благодаря этому случайное распределение будет каждый раз одним и тем же. Это позволяет проще отслеживать работу сети после внесения изменений в код.
syn0 = 2*np.random.random((3,1)) – 1
Матрица весов сети. syn0 означает «synapse zero». Так как в реализуемой нейросети всего два слоя, вход и выход, то необходима одна матрица весов, которая их свяжет. Вектор l0 имеет размер 3, а l1 – 1. Поскольку все узлы в l0 связываются со всеми узлами l1, то для этого необходима матрица размерности (3, 1). Такая матрица инициализируется случайным образом, и среднее значение равно нулю. За этим стоит достаточно сложная теория.
for iter in range(10000):
l0 = X
После этих строчек начинается основной код тренировки сети. Цикл с кодом повторяется многократно и оптимизирует сеть для набора данных.
Первый слой, l0, – это просто данные. В X содержится 4 тренировочных примера. Нейронная сеть обрабатывает их все и сразу – это называется групповой тренировкой [full batch].
l1 = nonlin(np.dot(l0,syn0))
Это шаг предсказания. Нейронная есть пытается предсказывать вывод на основе ввода. Далее будет оцениваться качество предсказания для исправления в нужную сторону. В строке содержится два шага. Первый делает матричное перемножение l0 и syn0. Второй передаёт вывод через сигмоиду.
В приведенном примере было загружено 4 тренировочных примера, и получено 4 догадки (матрица 4х1). Каждый вывод соответствует догадке сети для данного ввода.
l1_error = y – l1
Поскольку в l1 содержатся догадки, можно сравнить их разницу с реальностью, вычитая её l1 из правильного ответа y. l1_error – вектор из положительных и отрицательных чисел, характеризующий «промах» сети.
l1_delta = l1_error * nonlin(l1,True)
Данная строка – это то, благодаря чему нейронная сеть может обучаться. Ее нужно разбирать по частям.
Первая часть: производная
nonlin(l1,True)
l1 представляет три этих точки, а код выдаёт наклон линий, показанных ниже. При больших значениях вроде x=2.0 (зелёная точка) и очень малые, вроде x=-1.0 (фиолетовая) линия имеют небольшой уклон. Самый большой угол у точки х=0 (голубая). Это имеет большое значение. Также заметно, что все производные лежат в пределах от 0 до 1.
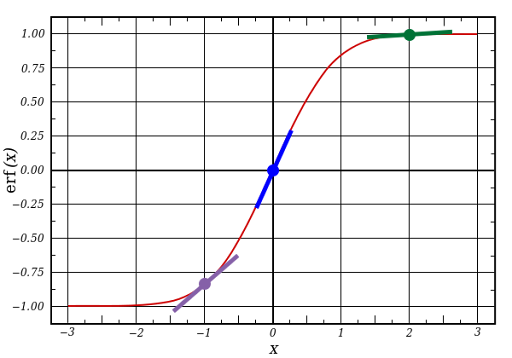
Полное выражение: производная, взвешенная по ошибкам
Математически существуют более точные способы, но в данном случае подходит и этот. l1_error – это матрица (4,1). nonlin(l1,True) возвращает матрицу (4,1). Они поэлементно перемножаются и на выходе тоже получаем матрицу (4,1), l1_delta.
Умножая производные на ошибки, уменьшаются ошибки предсказаний, сделанных с высокой уверенностью. Если наклон линии был небольшим, то в сети содержится либо очень большое, либо очень малое значение. Если догадка в сети близка к нулю (х=0, у=0,5), то она не особенно уверенная. Неуверенные предсказания обновляются и сохраняются предсказания с высокой уверенностью, умножая их на величины, близкие к нулю.
syn0 += np.dot(l0.T,l1_delta)
Далее сеть обновляет свои веса и переходит на следующую эпоху по циклу.
Нейросеть в три слоя
import numpy as np
def nonlin(x,deriv=False):
if(deriv==True):
return x*(1-x)
return 1/(1+np.exp(-x))
X = np.array([[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]])
y = np.array([[0],
[1],
[1],
[0]])
np.random.seed(1)
# randomly initialize our weights with mean 0
syn0 = 2*np.random.random((3,4)) – 1
syn1 = 2*np.random.random((4,1)) – 1
for j in range(60000):
# Feed forward through layers 0, 1, and 2
l0 = X
l1 = nonlin(np.dot(l0,syn0))
l2 = nonlin(np.dot(l1,syn1))
# how much did we miss the target value?
l2_error = y – l2
if (j% 10000) == 0:
print(“Error:” + str(np.mean(np.abs(l2_error))))
# in what direction is the target value?
# were we really sure? if so, don’t change too much.
l2_delta = l2_error*nonlin(l2,deriv=True)
# how much did each l1 value contribute to the l2 error (according to the weights)?
l1_error = l2_delta.dot(syn1.T)
# in what direction is the target l1?
# were we really sure? if so, don’t change too much.
l1_delta = l1_error * nonlin(l1,deriv=True)
syn1 += l1.T.dot(l2_delta)
syn0 += l0.T.dot(l1_delta)
Error:0.496410031903
Error:0.00858452565325
Error:0.00578945986251
Error:0.00462917677677
Error:0.00395876528027
Error:0.00351012256786
Переменные и их описания
X – матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
l2 – финальный слой, это наша гипотеза. По мере тренировки должен приближаться к правильному ответу
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
syn1 – второй слой весов, Synapse 1, объединяет l1 с l2.
l2_error – промах сети в количественном выражении
l2_delta – ошибка сети, в зависимости от уверенности предсказания. Почти совпадает с ошибкой, за исключением уверенных предсказаний
l1_error – взвешивая l2_delta весами из syn1, мы подсчитываем ошибку в среднем/скрытом слое
l1_delta – ошибки сети из l1, масштабируемые по уверенности предсказаний. Почти совпадает с l1_error, за исключением уверенных предсказаний
Данный код представляет собой предыдущую реализацию нейронной сети, сложенную в два слоя один над другим. Выход первого слоя l1 – это вход второго слоя. Что-то новое есть лишь в следующей строке.
l1_error = l2_delta.dot(syn1.T)
Нейросеть использует ошибки, взвешенные по уверенности предсказаний из l2, чтобы подсчитать ошибку для l1. В итоге получается ошибка, взвешенная по вкладам – подсчитывается, какой вклад в ошибки в l2 вносят значения в узлах l1. Этот шаг и называется обратным распространением ошибок. Затем обновляются веса syn0, используя тот же алгоритм, что и в варианте с нейросетью из двух слоёв.
Источник: http://iamtrask.github.io/2015/07/12/basic-python-network/ https://habr.com/ru/articles/271563/