У дадзеным курсе будзе апісаны алгарытм зваротнага распаўсюджвання памылак на прыкладзе двух невялікіх нейронных сетак, рэалізаваных на Python.

 

Кожная нейронная сетка, якая трэніруецца праз адваротнае распаўсюджванне (backpropagation), спрабуе выкарыстоўваць уваходныя даныя для прагназавання выходных.

 

Адваротнае распаўсюджванне ў самым простым выпадку разлічвае статыстычную адпаведнасць паміж уваходнымі і выходнымі данымі для стварэння мадэлі.

 

Нейрасеткі ў два слоі

 

import numpy as np

 

# sigmoid function

def nonlin(x,deriv=False):

    if(deriv==True):

        return x*(1-x)

    return 1/(1+np.exp(-x))

    

# input dataset

X = np.array([  [0,0,1],

                [0,1,1],

                [1,0,1],

                [1,1,1] ])

    

# output dataset            

y = np.array([[0,0,1,1]]).T

 

# seed random numbers to make calculation

# deterministic (just a good practice)

np.random.seed(1)

 

# initialize weights randomly with mean 0

syn0 = 2*np.random.random((3,1)) – 1

 

for iter in range(10000):

 

    # forward propagation

    l0 = X

    l1 = nonlin(np.dot(l0,syn0))

 

    # how much did we miss?

    l1_error = y – l1

 

    # multiply how much we missed by the 

    # slope of the sigmoid at the values in l1

    l1_delta = l1_error * nonlin(l1,True)

 

    # update weights

    syn0 += np.dot(l0.T,l1_delta)

 

print(“Output After Training:”)

print(l1)

 

Output After Training:

[[ 0.00966449]

 [ 0.00786506]

 [ 0.99358898]

 [ 0.99211957]]

 

Зменныя і іх апісанні.

 

X – матрыца ўваходнага набору даных; радкі – трэніровачныя прыклады

y – матрыца выхаднога набору даных; радкі – трэніровачныя прыклады

l0 – першы слой сеткі, вызначаны ўваходнымі данымі

l1 – другі слой сеткі або схаваны слой

syn0 – першы слой вагаў, Synapse 0, аб’ядноўвае l0 з l1.

“*” – паэлементнае множанне – два вектары аднаго памеру памнажаюць адпаведныя значэнні, і на выхадзе атрымліваецца вектар такога ж памеру

“-” – паэлементнае адніманне вектараў

1. dot (y) – калі x і y – гэта вектары, то на выхадзе атрымаецца скалярны твор. Калі гэта матрыцы, то атрымаецца перамнажэнне матрыц. Калі матрыца толькі адна з іх – гэта перамнажэнне вектара і матрыцы.

 

Разбор кода парадкова

 

import numpy as np

 

Гэтым радком імпартуецца numpy, бібліятэка лінейнай алгебры.

 

def nonlin(x,deriv=False)

 

Дадзеная функцыя стварае «сігмоіду». Яна ставіць у адпаведнасць любы лік значэння ад 0 да 1 і пераўтварае колькасці ў верагоднасці, а таксама мае некалькі іншых карысных для трэніроўкі нейрасеткі ўласцівасцяў.

Гэта функцыя таксама ўмее выдаваць вытворную сігмоіды (deriv=True). Гэта адно з яе карысных уласцівасцяў. Калі выхад функцыі – гэта пераменная out, тады вытворная будзе out * (1-out).

 

X = np.array([  [0,0,1],

                [0,1,1],

                [1,0,1],

                [1,1,1] ])

 

Ініцыялізацыя масіва ўваходных даных у выглядзе numpy-матрыцы. Кожны радок – трэніровачны прыклад. Слупкі – гэта ўваходныя вузлы. У дадзеным выпадку атрымліваецца 3 уваходныя вузлы ў сеткі і 4 трэніровачныя прыклады.

 

y = np.array([[0,0,1,1]]).T

 

Ініцыялізуе выходныя даныя. “T ”  – функцыя транспанавання. Пасля транспанавання ў матрыцы y ёсць 4 радкі з адным слупком. Як і ў выпадку ўваходных даных, кожны радок – гэта трэніровачны прыклад, і кожны слупок (у дадзеным выпадку адзін) – выходны вузел. У сетцы атрымліваецца 3 ўваходы і 1 выхад.

 

np.random.seed(1)

 

Дзякуючы гэтаму, выпадковае размеркаванне будзе кожны раз адным і тым жа. Гэта дазваляе прасцей адсочваць працу сеткі пасля ўнясення змяненняў у код.

 

syn0 = 2*np.random.random((3,1)) – 1

 

Матрыца вагаў сеткі. syn0 азначае “Synapse zero”. Бо ў рэалізуемай нейрасетцы ўсяго два слоі, уваход і выхад, то неабходна адна матрыца вагаў, якая іх звяжа. Вектар l0 мае памер 3, А l1-1. Паколькі ўсе вузлы ў l0 звязваюцца з усімі вузламі l1, то для гэтага неабходна матрыца памернасці (3, 1). Такая матрыца ініцыялізуецца выпадковым чынам, і сярэдняе значэнне роўнае нулю. За гэтым стаіць даволі складаная тэорыя.

 

for iter in range(10000):

    l0 = X

 

Пасля гэтых радкоў пачынаецца асноўны код трэніроўкі сеткі. Цыкл з кодам паўтараецца шматразова і аптымізуе сетку для набору даных.

Першы слой, l0, – гэта проста даныя. У X змяшчаецца 4 трэніровачныя прыклады. Нейронная сетка апрацоўвае іх усе і адразу – гэта называецца групавой трэніроўкай [full batch].

 

l1 = nonlin(np.dot(l0,syn0))

 

Гэта крок прадказання. Нейронная сетка спрабуе прадказваць выснову на аснове ўводу. Далей будзе ацэньвацца якасць прадказання для выпраўлення ў патрэбны бок. У радку ўтрымліваюцца два крокі. Першы робіць матрычнае перамнажэнне l0 і syn0. Другі перадае выснову праз сігмоіду.

 

У прыведзеным прыкладзе было загружана 4 трэніровачныя прыклады, і атрымана 4 здагадкі (матрыца 4х1). Кожная выснова адпавядае здагадцы сеткі для дадзенага ўводу.

 

      l1_error = y – l1

 

Паколькі ў l1 ўтрымліваюцца здагадкі, можна параўнаць іх розніцу з рэальнасцю, адымаючы яе l1 з правільнага адказу y. l1_error – вектар з станоўчых і адмоўных лікаў, які характарызуе «промах» сеткі.

 

       l1_delta = l1_error * nonlin(l1,True)

 

Дадзены радок – гэта тое, дзякуючы чаму нейронная сетка можа навучацца. Яе трэба разбіраць па частках.

 

Першая частка: вытворная

 

nonlin(l1,True)

 

l1 ўяўляе тры гэтыя кропкі, А код выдае нахіл ліній, паказаных ніжэй. Пры вялікіх значэннях накшталт x=2.0 (зялёная кропка), і вельмі малых, накшталт x=-1.0 (фіялетавая) лінія мае невялікі ўхіл. Самы вялікі кут у пункце х=0 (блакітная). Гэта мае вялікае значэнне. Таксама прыкметна, што ўсе вытворныя ляжаць у межах ад 0 да 1.

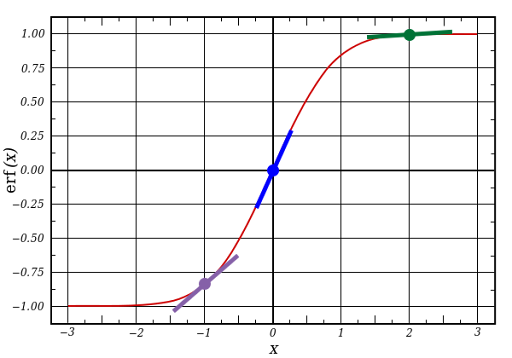
Поўны выраз: вытворная, узважаная па памылках

 

Матэматычна існуюць больш дакладныя спосабы, але ў дадзеным выпадку падыходзіць і гэты. l1_error – гэта матрыца (4,1). nonlin (l1,True) вяртае матрыцу (4,1). Яны паэлементна перамнажаюцца і на выхадзе таксама атрымліваем матрыцу (4,1), l1_delta.

 

Памнажаючы вытворныя на памылкі, памяншаюцца памылкі прадказанняў, зробленыя з высокай упэўненасцю. Калі нахіл лініі быў невялікім, то ў сетцы змяшчаецца альбо вельмі вялікае, альбо вельмі малое значэнне. Калі здагадка ў сетцы блізкая да нуля (х =0, у=0,5), то яна не асабліва ўпэўненая. Няўпэўненыя прадказанні абнаўляюцца і захоўваюцца прадказанні з высокай упэўненасцю, памнажаючы іх на велічыні, блізкія да нуля.

 

      syn0 += np.dot(l0.T,l1_delta)

 

Далей сетка абнаўляе свае вагі і пераходзіць на наступную эпоху па цыкле.

 

Нейрасеткі ў тры слаі

 

import numpy as np

 

def nonlin(x,deriv=False):

if(deriv==True):

    return x*(1-x)

return 1/(1+np.exp(-x))

    

X = np.array([[0,0,1],

            [0,1,1],

            [1,0,1],

            [1,1,1]])

                

y = np.array([[0],

[1],

[1],

[0]])

 

np.random.seed(1)

 

# randomly initialize our weights with mean 0

syn0 = 2*np.random.random((3,4)) – 1

syn1 = 2*np.random.random((4,1)) – 1

 

for j in range(60000):

 

# Feed forward through layers 0, 1, and 2

    l0 = X

    l1 = nonlin(np.dot(l0,syn0))

    l2 = nonlin(np.dot(l1,syn1))

 

    # how much did we miss the target value?

    l2_error = y – l2

    

    if (j% 10000) == 0:

        print(“Error:” + str(np.mean(np.abs(l2_error))))

        

    # in what direction is the target value?

    # were we really sure? if so, don’t change too much.

    l2_delta = l2_error*nonlin(l2,deriv=True)

 

    # how much did each l1 value contribute to the l2 error (according to the weights)?

    l1_error = l2_delta.dot(syn1.T)

    

    # in what direction is the target l1?

    # were we really sure? if so, don’t change too much.

    l1_delta = l1_error * nonlin(l1,deriv=True)

 

    syn1 += l1.T.dot(l2_delta)

    syn0 += l0.T.dot(l1_delta)

 

Error:0.496410031903

Error:0.00858452565325

Error:0.00578945986251

Error:0.00462917677677

Error:0.00395876528027

Error:0.00351012256786

 

Зменныя і іх апісанні

 

X – матрыца ўваходнага набору даных; радкі –трэніровачныя прыклады

y – матрыца выхаднога набору даных; радкі – трэніровачныя прыклады

l0 – першы слой сеткі, вызначаны ўваходнымі данымі

l1 – другі слой сеткі, або схаваны слой

l2 – фінальны слой, гэта наша гіпотэза. Па меры трэніроўкі павінен набліжацца да правільнага адказу

syn0 – першы слой вагаў, Synapse 0, аб’ядноўвае l0 з l1.

syn1 – другі слой вагаў, Synapse 1, аб’ядноўвае l1 з l2.

l2_error – промах сеткі ў колькасным выразе

l2_delta – памылка сеткі, у залежнасці ад упэўненасці прадказання. Амаль супадае з памылкай, за выключэннем упэўненых прадказанняў

l1_error – узважваючы l2_delta вагамі з syn1, мы падлічваем памылку ў сярэднім/схаваным слоі

l1_delta – памылкі сеткі з l1, маштабуюцца па ўпэўненасці прадказанняў. Амаль супадае з l1_error, за выключэннем упэўненых прадказанняў

 

Дадзены код уяўляе сабой папярэднюю рэалізацыю нейроннай сеткі, складзеную ў два слаі адзін над іншым. Выхад першага слоя l1 – гэта ўваход другога слоя. Нешта новае ёсць толькі ў наступным радку.

 

   l1_error = l2_delta.dot(syn1.T)

 

Нейрасетка выкарыстоўвае памылкі, узважаныя па ўпэўненасці прадказанняў з l2, каб падлічыць памылку для l1. У выніку атрымліваецца памылка, узважаная па ўкладах – падлічваецца, які ўклад у памылкі ў l2 уносяць значэнні ў вузлах l1. Гэты крок і называецца зваротным распаўсюджваннем памылак. Затым абнаўляюцца вагі syn0, выкарыстоўваючы той жа алгарытм, што і ў варыянце з нейрасеткамі з двух слаёў.

Крыніца: http://iamtrask.github.io/2015/07/12/basic-python-network/ https://habr.com/ru/articles/271563/